C. B. Fisk, Inc., Opus 133
The C. B. Fisk, Inc., shop, located near sea level in Gloucester, Massachusetts, had to carefully consider the delivery of their Opus 133 to an altitude of 2,127 meters (6,978 feet) at First Presbyterian Church, Santa Fe, New Mexico. Would that affect its sound? With 74% of the world’s population living below an altitude of 500 meters (1,640 feet), the effects are unnoticed, and we rarely have to deal with this.1 Others have addressed this problem, and we can find excellent guidance in an article by James W. Toevs using Fisk’s Opus 133 as an example, where he noted that altitude had no effect on “basic intonation” (here meaning “pitch,” not “voicing”), but had a “significant effect [on] . . . pre-voicing and voicing.”2 I am a voicer, I live at 5,000 feet altitude, and I want to understand how altitude affects the sound and the voicing. We can find answers with Hartmut Ising, a man who thought very deeply about voicing.
Toevs explains that at higher altitudes air will be less dense, and at sea level the voicing must be done at a higher pressure than the intended pressure at altitude. The compensation is simple: find the ratio of the air density at the workshop to the air density at altitude, and then multiply it by the desired pressure at altitude to find the correct pressure for voicing in the shop. In the example of Fisk’s Opus 133, the air density at Santa Fe is 77% of that at sea level, and we get a ratio of 1 / 0.77 = 1.3. Fisk’s desired pressure at altitude was 76 mm water column, so at sea level the pressure needed for voicing was 76 mm x 1.3 = 99 mm. As any voicer knows, that is a big change in wind pressure and a lot more power!
Hartmut Ising and Johan Liljencrants
The Fisk example shows us how to compensate for voicing at different altitudes, but if we want to understand how the voicing and sound is affected, it might help to explain the need to adjust wind pressure.
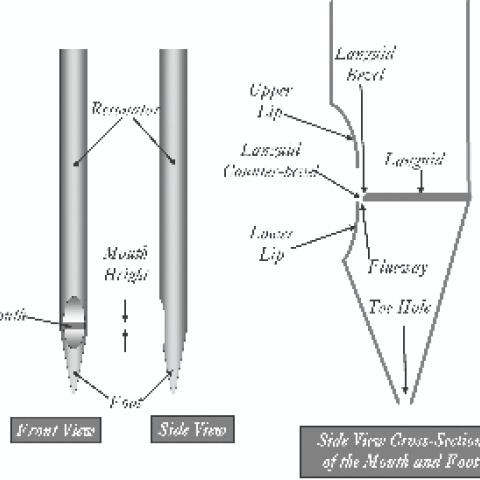
In a 1971 internal publication of the Walcker firm, Hartmut Ising proposed an equation to show how the timbre of a pipe (a primary goal of voicing) is affected by its pitch, the height of its mouth (also known to voicers as “cutup”), the depth of its flueway, and the velocity of air (this last term was transformed by Johan Liljencrants into air density and wind pressure).3 For those not familiar with these terms, Figure 1 illustrates the front, side, and cross-section views of an organ pipe, showing its mouth height H and its flueway depth D. This equation is rarely seen, but it gives profound insight into many aspects of voicing.
I am going to take a great risk here by showing the somewhat intimidating Ising equation (in its form by Liljencrants). This is where readers will normally storm for the exits, but bear with me, I will do all the math for you in Excel, and I will show you what it can teach us:
[Ising equation]
I is the timbre of a pipe—the German word for “voicing” is Intonation. An I value of 1 is the timbre of a smooth flute. A value of 2 is an optimal state for the “shortest duration between the opening of the pipe valve and reaching the steady pipe sound (fundamental plus overtones).”4 In this state the timbre of a pipe also has more power in its harmonics, i.e., it is more like a principal and brighter. A value of 3 is the point where the harmonics have become so strident and powerful relative to the fundamental that the pipe overblows to the octave (strings can operate in this region with help from devices like roller beards to prevent overblowing). Most organ pipes are voiced in a range of values from about 0.8 (a very smooth flute with delicate harmonics) to about 2.3 (a principal with very well-developed harmonics and brightness).5
F is the frequency of the pitch in Hz.
D is the depth of the flueway in meters.
H is the height of the mouth in meters.
P is the wind pressure in Pascals, or N/m2. Organ pressure is measured by the height of a water column, and 1 mm of pressure = 9.80665 Pascals. This is the term we will vary to see how it affects the timbre of the pipe I.
ρ is the density of air in kg/m3, which is 1.2 kg/m3 under standard conditions at sea level. This is the term we will adjust for different altitudes.
The beauty of Ising’s equation is that it lets us “hear” the changes to the timbre of a pipe’s voicing when we change its altitude or its pressure. Let’s see what it can show us.
Air density at different altitudes is a subject with complex compensations that include temperature and humidity. Figure 2 shows online data that yielded air densities ρ in very close agreement with Toev’s example.6
We are now ready to create the Excel table shown in Figure 3, and we will begin with a sea level air density ρ of 1.20 in the last column. A full range of pipes from 16′ to 1⁄8′ are shown in column 1, and the frequencies F of the pitches of those pipes are seen in column 3. The flueway depths D in column 4 are typical of the principal chorus voicing of the Isnards at Saint-Maximin, and the mouth heights H in column 5 are all Normal Scale.7 In column 6 the pressure P in the foot of the pipes is adjusted to 35 mm (343.2 Pascals). The Ising equation now calculates timbre values I of 2.21, shown by the red arrow in column 2.
The flueway depths D were fine-tuned to get the same I values for all pitches (with minor rounding variations). This is probably in the ballpark for the Isnard sound. The bellows pressure of the Isnard organ is 83 mm, but the toes of the flue pipes are closed and the actual pressure in their feet is far lower.8 Figure 3 represents voicing at sea level.
Now we are ready to see what happens if we adjust our altitude to 1,500 meters by changing the air density ρ from a value of 1.20 to 1.00 in the last column in Figure 4. We are not changing the sea level voicing in the flueways, mouth heights, or wind pressure. The change to the timbre I is a revelation.
The timbre I increases to a value of 2.42 for all pitches. This is a much brighter and more powerful sound, and it is not what the voicer intended at sea level! While I do not recommend this as a solution (it would involve a great deal of work), we could raise the mouth heights (cutups) on all of the pipes to restore the timbre of the original sound. For example, in Figure 5 we see the new mouth heights H (in red font) that would restore the timbre of the pipes at 1,500 meters altitude to an I value of 2.21.
The mouth heights and flueways in this table are noted in meters, so the mouth height on the 16′ pipe is 54.5 mm, and so on for the other pitches. You can compare these heights (cutups) to the table in Figure 4—very small changes in mouth height make big changes in the timbre. The point of this example is to show that mouth height can be adjusted to keep a constant timbre at different levels of power.9
The much better solution for moving an organ to a higher altitude, just as Toevs suggests, is to lower the wind pressure. For our new example, we find the ratio of the air densities at 1,500 meters altitude and sea level: 1.0 / 1.2 = 0.83. Using this ratio, our new lower wind pressure is 0.83 x 35 mm = 29.1 mm. Figure 6 demonstrates our original sea-level voicing, but the air density ρ is 1.00 for 1,500 meters altitude in the last column, and our new lower wind pressure P of 29.1 mm (285.4 Pascals) is shown by the red arrows at the right). Figure 6 now calculates an I timbre value of 2.21 at 1,500 meters altitude, the exact timbre we had at sea level on the higher pressure with our original voicing!
Higher altitude brightens the timbre
The Ising equation confirms the Fisk method of altitude compensation with wind pressure, and it shows why we have to compensate for it—while we might be gasping for breath at higher altitudes, the sound of a pipe organ gets brighter. If we reduce the wind pressure in the bellows with higher altitude, we can keep the same timbre at any altitude with the same voicing. This is a key insight from Ising, and his equation works in the real world of voicing.9
The final piece of the puzzle
We might correctly surmise from the Ising equation that the power of both the fundamental and the harmonics increases with altitude, and the power of the harmonics will increase faster than the fundamental, making the sound brighter. Adjusting our wind pressure lower corrects both the timbre and the power. But there is one more crucial effect at play here: the intensity of sound decreases in rough proportion with the air density.10 This means that power will drop with altitude.
And this is why Fisk chose a target pressure for their normal power at altitude and raised that pressure at sea level for pre-voicing. They simply voiced the pipes at sea level with normal timbre and more power on higher pressure. Then, when the pressure was reduced at altitude, the normal timbre was maintained and the power dropped to normal as well. Now we know how the sound and voicing of organ pipes are affected by altitude and why the Fisk method works.
What this means for the organ builder
The bottom line here is very important. Once an organ is voiced at a desired power level, timbre, and pressure at a specific altitude, it cannot maintain both its timbre and its power at a different elevation with the same voicing.
Pressure can be adjusted lower if the organ is moved to a higher elevation to keep the timbre the same, but the power will be lower. If the original pressure is maintained, the power will be the same, but the timbre will be much brighter (requiring higher cutups to restore the timbre).
Pressure can be adjusted higher if the organ is moved to a lower elevation to keep the timbre the same, but the power will be higher. If the original pressure is maintained, the power will be the same, but the timbre will be much duller (and cutups are not easily lowered).
A graph for altitude compensation
If you are able to plan ahead for a change in altitude, I have used the Ising equation and the air densities from Figure 2 to do the calculations for you in the graph in Figure 7. This graph will give a constant timbre and power for flue pipes spanning a range of altitudes from sea level to 2,500 meters (8,202 feet). See Figure 7 for instructions on its use and a worked example.
The graph in a nutshell
Voicing at a lower altitude for delivery to a higher altitude: Adjust the pressure higher than normal and voice for higher power with normal timbre; drop to the target pressure at higher altitude. The timbre and power will be normal. Voicing at a higher altitude for delivery to a lower altitude: Adjust the pressure lower than normal and voice for lower power with normal timbre; raise to the target pressure at lower altitude. The timbre and power will be normal.
Notes & References
1. Joel E. Cohen and Christopher Small, “Hypsographic demography: The distribution of human population by altitude,” Proceedings of the National Academy of Sciences of the United States of America, November 24, 1998, 95 (24), pp. 14009–14014.
2. James W. Toevs, “Organ Acoustics at High Altitudes,” The Diapason, October 2009, p. 31.
3. Hartmut Ising, “Erforschung und Planung des Orgelklanges,” Walcker Hausmitteilung, no 42, Juni 1971, pp. 38–57. Johan Liljencrants shows a form of this equation on the website www.fonema.se, accessed on October 18, 2020, which contains not only Liljencrant’s work but also the original Ising article. On this website we see that Liljencrants modified Ising’s original equation to use pressure and air density rather than velocity, making the equation more easily used by the organbuilder. Here is his transformation of Ising’s equation:
4. Personal communication from Dr. Hartmut Ising, October 2020. Previous literature has translated I = 2 as an optimal state for the fundamental, but did not define what was optimal about it. Dr. Ising continued to clarify this: “for I = 2 the transient of the sound is optimal (Einschwingvorgang).”
5. John Nolte, “Scaling Pipes in Wood,” ISO Journal, no. 36, December 2010, pp. 8–19. The original website referenced in this article by Nolte that posted the English translation of Ising’s equation by Liljencrants and his description of the range of values for I has disappeared. The website, www.fonema.se, contains much of this information. See also note 4 above.
6. www.engineeringtoolbox.com/air-altitude-density-volume-d_195.html, accessed August 25, 2020. The baseline at sea level assumes 20 deg C temperature, 40% humidity, and standard pressure.
7. Michael McNeil, The Sound of Pipe Organs, CC&A, 2014, Amazon.com, pp. 68–72. This chapter explains the derivation and use of the Normal Scale for cutups and displays a chart for all pitches from 32′ to 1⁄8′.
8. The scintillating Isnard reeds have far more open toes and their thicker tongues are more effective with the higher bellows pressure. The higher pressure also compensates for pressure losses in the tubing to the many offset pipes, which have much more open toes than the pipes on the windchests. Open toe voicing of flue pipes on even modest wind pressures requires compensation in the flueway depths, just as we find in neo-Baroque voicing. The warmth of French Classical voicing resides in its open flueways.
9. The Sound of Pipe Organs, pp. 77–84. A spectral analysis of a pipe’s sound measures the power of its harmonics and objectively quantifies its timbre. This chapter uses Ising’s equation to show how timbre, pressure, and cutup are related, using examples of spectral data from organ pipes taken with a state-of-the-art (in 1975) spectrum analyzer.
10. www.physics.stackexchange.com/questions/672/what-is-the-relation-of-sound-propagation-to-air-pressure, accessed October 3, 2020. Sound intensity is roughly proportional to the air density.
The equation for sound intensity is I = ξ2 ω2 c ρ, and I here represents intensity, not Ising’s I for timbre.
I = intensity
ξ = particle displacement
ω = frequency
c = speed of sound
ρ = density of air
