Michael McNeil has designed, constructed, voiced, and researched pipe organs since 1973. Stimulating work as a research engineer in magnetic recording paid the bills. He is working on his Opus 5, which explores how an understanding of the human sensitivity to the changes in sound can be used to increase emotional impact. Opus 5 includes double expression, a controllable wind dynamic, chorus phase shifting, and meantone. Stay tuned.

Editor’s note: The Diapason offers here a feature at our digital edition—four sound clips. Any subscriber can access this by logging into our website (thediapason.com), click on Magazine, then this issue, View Digital Edition, scroll to this page, and click on each <soundclip> in the text.
Many American organists have traveled to Europe and heard the sounds of older organs that make Bach a revelation. American organ building was for much of its history rooted in the Anglican tradition and the Romantic sounds of organbuilders like Ernest M. Skinner, and neither of those great art forms are an ideal medium for Bach. Tentative steps in the Anglican tradition were made as early as the 1930s to recreate this European sound, but they did not amount to a revelation. The revelation occurred with a British-born virtuoso, E. Power Biggs, who brought a sound to America that would convincingly play Bach in the form of an organ built by D. A. Flentrop. Biggs paid for this organ out of his own pocket and in 1958 found a home for it in the very reverberant acoustics of what was known at the time as the Busch Reisinger Museum.1 His recordings of this Flentrop energized the budding Organ Reform Movement in the United States and inspired many American organbuilders. Listen to the end of the Fugue in A Minor, BWV 543ii <Soundclip 1>.
Dirk Andries Flentrop (1910–2003) worked in his father’s organbuilding shop and with Theodor Frobenius in Denmark, eventually taking over his father’s business. He was intensely interested in classical organ design, and he gave a lecture at a very young age in 1927 in which he promoted the use of mechanical action and slider windchests.2 A conversation with Flentrop in the 1970s turned to his earlier career, and he recalled that he was traveling on a streetcar in Rotterdam when bombs started falling on that city in World War II. Everyone on the streetcar agreed there was no point in getting off, and they continued traveling to their destinations as bombs fell. The date was May 10, 1940, the year he took over his father’s business. I sailed with my parents on the SS Rotterdam in 1964 and still remember the shock of seeing upturned docks as we approached the harbor at Rotterdam and whole city blocks of uncleared rubble decades after the bombing.
Flentrop’s sound
The sound of pipe organs can be described subjectively and objectively. Subjectively, the sound of D. A. Flentrop is bright and “instrumental,” where individual pipes in the principal chorus have rich harmonic content. This is very different from what is today called vocale voicing, which emphasizes less harmonic power. Flentrop’s richly harmonic sound creates a scintillating principal chorus with clarity of pitch.
A key component of this sound, and a strong departure from the Romantic and Anglican traditions, is the expression of “chiff.” E. Power Biggs described chiff as the articulate “ictus” of a sound, adding clarity to rhythm and contrapuntal harmony. Chiff is not just percussive noise. It consists of higher natural harmonics to which the human ear is very sensitive, quickly defining the pitch. Flentrop was a master of this percussive speech, and it was always musical and fast. Chiff can be modulated with a sensitive mechanical action and low wind pressures (i.e., with little or no key pluck). Biggs was adept at this on his Flentrop, easing the pallets open for a smooth treble line while crisply opening the pallets to delineate inner voices with more chiff.
Later expressions of this articulation in what became known as neo-Baroque voicing are often heard as a slow, gulping sound. You never hear slow, gulping speech in a Flentrop organ, and as the data will show, Flentrop’s voicing exhibits no relationship to neo-Baroque voicing recipes.3
There is ample evidence that much of D. A. Flentrop’s sound is based on examination of the work of Arp Schnitger, and Schnitger’s sound is much more instrumental in character than modern vocale voicing. The similarity to Schnitger extends also to the design of the reeds, whose basses are the source of a smooth and powerful fundamental.
Flentrop organs have considerable presence, due in large part to the shallowness of the casework found in all of his organs. Flentrop related that the maximum depth of a case should be no deeper than the reach of an arm from the back doors of the case to its façade pipes. Deep cases and chambers will tend to absorb sound, especially the higher harmonics that create the sense of presence. I find it interesting that unaltered manual divisions of Cavaillé-Coll organs, while using higher pressures with Romantic scaling and voicing, almost never exceeded twelve stops and always used slider chests with mechanical action, reflecting some of the important design features of Flentrop organs.
The generosity of D. A. Flentrop
D. A. Flentrop was secure in his knowledge and very willing to share it. I was the recipient of his generosity on several occasions when he toured the United States with his senior voicer, Sijmen “Siem” Doot, to maintain and tune his organs. Doot, born in 1924, entered Flentrop’s service in 1939 and retired in 1988. Ed Lustig at Flentrop Orgelbouw confirmed that Franz Rietsch, Rob Oudejans, Johannes Steketee, and Doot assembled the Flentrop organ in Saint Mark’s Episcopal Cathedral, Seattle, Washington, in 1965, while Steketee and Doot remained to voice the organ. The voicing data in this article is a testament to their skill. I was introduced to Flentrop by Albert Campbell in 1971. After scouring the literature and finding mostly subjective opinions with very little data, I quickly discovered that Flentrop was genuinely interested in answering the detailed questions of a budding organbuilder. When I asked him if he would grant me permission to take measurements of his organs, he replied, “imitation is the finest form of flattery. Your ears will be different than mine, and you will use your observations to find your own sound.” He was right, but it took quite some time before I began to understand some of those observations, and the data continues to generate insights.
I again met Flentrop in the Campbell home after completion of my Opus 1, and by that time I had learned enough to ask deeper questions. Flentrop had nearly completed the tuning of his organ at the University of California, Santa Barbara, and in a further gesture of generosity, Flentrop said, “If you finish the cone tuning of the Hoofdwerk Mixtuur, we can answer your questions.” I agreed to finish the tuning work on the Flentrop organ, and both he and Mr. Doot spent the whole day answering my questions.
Flentrop slider windchests
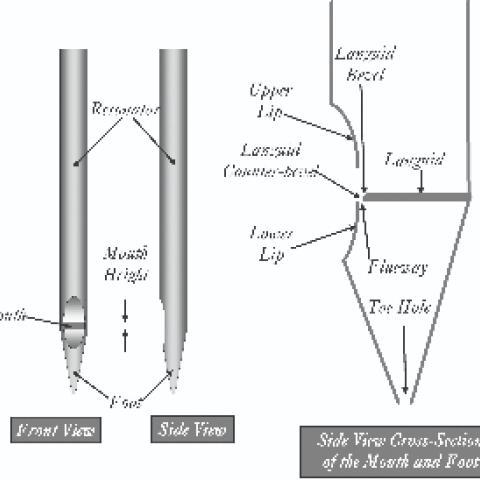
D. A. Flentrop organs have exclusively featured mechanical key action and slider windchests since 1949. Stop actions were mechanical, as well, and only in his larger organs do we find electric slider motors and combination actions. Organbuilders who looked to the literature for the design principles of slider chests in the 1970s often found the effort frustrating. Flentrop willingly shared a great deal of his design practice. In Figure 1 we see a drawing made by the author from notes of a conversation with Flentrop regarding channel design. Flentrop recommended that the cross-sectional area of the key channel should have about 20–30% more area than the combined areas of all of the pipe toes it would need to wind. A small vent hole at the end of the channel served two functions—to prevent ciphering and to dampen resonances in the channel that would interfere with reeds. Reeds that are equal in length to the channel that feeds wind to them may get much louder, and those not quite equal to that length may get much weaker and more dull in timbre from channel resonance. I noted that the bottom of the key channels in the Flentrop organ at the University of California, Santa Barbara, were covered in a thick paper that had pin pricks in a few channels in various positions, likely done to reduce channel resonance.
Flentrop stated that pallets did not need to exceed 200 millimeters (about eight inches) in length, but I have found much longer pallets in Hook organs. I did not ask how to trade off key channel widths and heights for a given area, nor the flow areas of the pallets, and these tradeoffs can be complex. Suffice it to say that the flow area of a pallet is the length of its opening times the distance the pallet is pulled open by the key (an open pallet has a triangle of flow at each side, and when combined, these triangles make a rectangle). It is also interesting to note that a pallet will not flow significantly more wind to a channel when its pull is more than half of the channel width (think about the height of those triangles that flow wind relative to the width of the channel). For a given pallet pull and a key channel width that is twice the pull, only a longer pallet will flow more wind to the channel.
The 1863 Hook organ at the former Church of the Immaculate Conception in Boston, Massachusetts, has roughly 460-millimeters-long pallets feeding 406-millimeters-long flue and reed channel openings in the Great bass octave (there are two pallets per note). The Romantic voicing of the Hook organ requires a very large volume of wind to feed its very deep flueways and very widely opened toes, which are much larger than Flentrop’s. At Saint Mark’s, Flentrop likewise used two pallets for the six bass notes of the Hoofdwerk, with pallet opening lengths of 155 millimeters, flue and reed channel widths of 21 millimeters and 17 millimeters, respectively, and a channel height of 79 millimeters. Readers who are interested in comparing the differences in the voicing of Flentrop and Hook organs can find the Hook data in The Diapason.4
Flentrop’s patented slider
Slider windchests in ancient organs often suffered from the advent of central heating. Topboard bearers are shimmed with layers of paper for a close fit between the slider, the windchest table on which it rests, and the topboard above it. With central heating and the resulting low humidity, shrinking wood caused these sliders to leak wind and impair the tuning. Many different forms of slider seals were invented in the twentieth century, most of which worked quite well. Flentrop’s system is patented and rather complex, but it is extremely reliable. Flentrop used two sliders, separated by springs with a leather-faced conduit for the wind between the two sliders. Figure 2 (see page 15) shows this slider seal mechanism in relation to the pallets, key channels, and topboards.
An objective approach to Flentrop’s sound
If you want to discover how to achieve a certain sound, it is often educational to closely observe the organs you like and those you do not. The objective differences will teach you what matters. Readers who want some perspective on the following Flentrop data will find a description of the voicing of several historic organs in The Diapason.5
The absolute minimum data needed to understand the sound of an organ is:
• pipe diameters (inside);
• mouth widths;
• toe diameters;
• mouth heights (also known as “cutups”)
• flueway depths.
Complete descriptions of these parameters can be found in the article mentioned above.6 In a nutshell, larger pipe diameters, wider mouth widths, larger toe diameters, and deeper flueways yield more power. Mouth heights control timbre, and higher mouths reduce harmonic power and brightness. Flutes typically have much higher mouths than more harmonically rich principals.
Wider scales produce an “ah” timbre, and narrower scales will progress towards an “ee” timbre, emphasizing higher harmonics. Flentrop stated that he used a constant scale of pipe diameters and mouth widths for the principal chorus in most environments and acoustics, which meant that he wanted a specific vowel timbre for all of the pipes at the same pitch and a specific power balance across the range of frequencies from bass to treble.
For different acoustics Flentrop used different pressures and voicing, adjusting the toe diameters and cutups. Ascending trebles were achieved in the toe diameters. Figure 3 shows Flentrop’s chorus scaling written in his own hand in 1971 with numerical values he had memorized.
Flentrop reeds were often made by the firm of Giesecke to Flentrop’s specifications. A description of the data needed to understand the sound of a reed can be found in an article in The Diapason.7 The author’s measurements of the Saint Mark’s reeds were not taken in sufficient detail to merit showing them. Flentrop reed designs are very similar to Schnitger’s and use tin-lead plates with restricted openings soldered to wide, lightly tapered, and deeply cut shallots for powerful, smooth basses. These typically transition to open, parallel shallots without plates in the tenor.
Taking the data at Saint Mark’s
I have been fortunate that many of those who are a gate to the access to some important organs have granted me permission to measure them. In 1972 that good fortune allowed me to take measurements of Flentrop’s organ at Saint Mark’s Episcopal Cathedral, Seattle, Washington, the organ Flentrop considered his largest by virtue of its 32′ façade pipes. The stoplist of the Saint Mark’s organ is easily found on the internet.8
The cathedral measures an estimated 150 feet in length and width, with a flat, wooden ceiling about 90 feet high. The walls are very thick concrete, yielding an acoustical reverberation of about five plainly audible seconds in the soprano range.9 The reverberation drops dramatically in the tenor and bass as a consequence of the very large windows, through which the lower frequencies easily pass.
Richard Frickmann, a life-long friend, and I drove over a thousand miles to visit this organ, and upon arrival in the early morning we sat in the pews in the empty cathedral, looking back at the organ. Glenn White, who maintained the organ, noticed our interest in this magnificent Flentrop and struck up a conversation. Learning that we were eager to find scaling data of the pipes, he questioned us for about five minutes and admitted that no one had taken the time to measure the pipework. He took us to the office and gave us the keys to the Flentrop casework, the organ loft, and the cathedral, asking that we return them when we were done. This was a stunning opportunity and one rarely offered. Mr. Frickmann and I took over fifty pages of data, interspersed with trips to the local twenty-four-hour pancake house to refuel with food and coffee. I had brought with me copies of scaling sheets and measuring tools, and Mr. Frickmann wrote down the numbers as I called them out from the walkways behind the windchests. After about twenty-four continuous hours of work, we handed in the keys to the office.
A word of caution on the data is in order. I took this data in 1972, very early in my career. I had experience with Flentrop’s organ at the University of California at Santa Barbara, and I understood basic scaling and data collection. But what I did not yet appreciate at the time was the importance of measuring the depth of the flueway. My general observations of the flueways of the Saint Mark’s organ were that “they tend to be consistent throughout the organ relative to pitch, much wider than current neo-Baroque work, but narrower than the voicing of the early American builders like Johnson and the Hooks.” Later measurements of Flentrop flueways provided a generalized model of the flueways for the Saint Mark’s organ. Please be aware that these are probably in the ballpark, but they are assumptions.
I was very careful in the handling of the pipes and making sure that their mouths faced in their original directions (this affects tuning on larger pipes whose mouths can be close to other pipes and shaded by them, lowering their pitch). The measurements of these pipes will have some inaccuracy from the time constraints. For larger pipes the measurements are likely better than +/- 1 millimeter, and for the very smallest pipes, about +/- 0.2 millimeter. The data is presented in halftone deviations from Normal Scale to make the relationships clear, as tables of numbers do not easily convey their meaning. These Normal Scales were published in the author’s article, “1863 E. & G. G. Hook Opus 322: Church of the Immaculate Conception, Boston, Massachusetts,” Part 1.10 Those who want actual measurements can use those tables to convert the Normal Scale data into dimensions, or they can email the author for a copy of the Excel spreadsheet with the more accurate raw dimensional data.11
The Hoofdwerk
Larger pipe diameters generate more power, and smaller diameters generate a brighter timbre. Flentrop’s principal chorus scales combine these factors into the sound he wanted. His scaling model in Figure 3 is seen as a dashed blue line in Figure 4. The model generally follows the Saint Mark’s data. As Flentrop noted, the mixtures are narrower. Flutes trend much wider as the pitch ascends.
Sound clips of the Saint Mark’s Flentrop in the digital edition of this article allow one to hear these power and timbre balances. They were derived from 1981 recordings of James Welch, organist, another life-long friend. The recording engineer, Dave Wilson, was known as one of the world’s best, and he recorded Welch on Flentrop organs. I was present in 1981 for the Saint Mark’s recordings, mostly to help with touching up the tuning of the reeds. I also made suggestions for stop registrations that ran counter to the prevailing wisdom of the time, dictating a minimal use of foundations to aid in clarity of pitch. This was not necessary on a Flentrop, whose foundations can be combined to any degree and still maintain clarity of pitch. Amassing foundations, as any Romantic organist knows well, is a source of rich chorus depth, and it is heard to great effect in Charles-Marie Widor’s “Andante cantabile” from Symphonie IV in <Soundclip 2>.
We made many experiments with microphone placement. The proper power balances of the different Flentrop divisions were finally achieved by placing microphones on very tall stands about twenty to thirty feet in front of the Rugwerk, the division that has the most presence for the congregation. Having been accustomed to the practice of using fast tempos in dry acoustics, Welch and I discussed appropriate tempos for the reverberant acoustic of Saint Mark’s. Borrowing headphones from the recording engineer to hear what the sound was like in the room at the microphones, he arrived at the tempo we hear in C. P. E. Bach’s Toccata and Fugue in D Minor, which takes full advantage of Saint Mark’s long reverberation <Soundclip 3>.
Late in the all-night recording session a note went dead in the Rugwerk. The organ had been in service for only sixteen years at this time, and a failure was unexpected. I pulled up the floor panels in the choir loft, which gave access to the Rugwerk trackers, and the culprit was a torn piece of weak leather that connected a long horizontal tracker at a suspension point. None of the other connectors showed the slightest sign of wear. I made a temporary fix, adjusted the action, and we continued recording well into the next morning.
Figure 5 shows the scales of the mouth widths, and these generally imitate the diameter scales. Normal Scale mouth widths are based on 1⁄4 of the circumferences of Normal Scale diameters, and as Flentrop almost exclusively used 1⁄4 mouths, we would expect a similarity to the diameter scales. Some of these mouth widths appear to be a bit wider than 1⁄4 of the circumference, and this may indicate that the pipes were slightly tapered, something I did not measure, and which is not uncommon. Inside diameters were measured at the top of the pipes. If the pipes have a slight taper, the true diameter scales at the bottom will be larger and will more closely match the Flentrop model in Figure 4, as well as the mouth scales in Figure 5.
Figure 6 shows mouth heights, or what is more commonly known as “cutups.” The cutup controls timbre. A higher mouth will reduce the harmonic content, and smooth flutes have higher cutups. These can be clearly seen in the lofty cutups of the 8′ Roerfluit. Normal Scale mouth heights are calculated as 1⁄4 of the Normal Scale Mouth Width, a common recipe in neo-Baroque voicing. In Figure 6 we see that Flentrop did not use this recipe. The Saint Mark’s cutups are much higher, and they have no relationship to the mouth width scales. They are also highly variable as a free voicing parameter. Flentrop raised the cutup until the desired timbre was achieved and the speech was fast. This is why you do not hear slow, gulping speech in a Flentrop organ.
The soaring cutups of the Roerfluit
The soaring cutups of the 8′ Roerfluit illustrate how Flentrop achieved a rich harmonic timbre in his principal chorus and a smoother, warmer timbre in the flutes. While Flentrop is noted for a brighter, “instrumental” timbre, which strongly implies lower cutups, Figure 6 clearly shows that his cutups were much higher than the neo-Baroque recipe. As an example, the cutup of the 8′ Roerfluit tenor C pipe in Figure 6 is +5 halftones, while its mouth width in Figure 5 is -5 halftones, revealing a cutup that is a stunning 10 halftones higher than the neo-Baroque recipe.
Figure 7 (see page 18) shows the relative flow of wind in the pipe toes. Larger pipe toes will flow more wind and yield more power. Received wisdom relates that Flentrop used “open toe” voicing, but Flentrop toes are in most cases quite restricted. Much more open toes can be found in Hook organs. Hook toe diameters also have high variability at a specific pitch, very unlike the more regular wind flow patterns we see with D. A. Flentrop and Gottfried Silbermann.13
The values in Figure 7 are toe constants, a number that represents relative flow. Flentrop suggested to me that a reasonable starting point for a toe diameter is the square root of its resonator diameter. The area of that closed toe represents a constant of “1,” and as you can see in Figure 7, Flentrop converged on that number at about 1′ pitch and increased the flow in both deeper and higher pitches. The area of the toe is proportional to the toe constant, i.e., a toe constant of “2” has twice the area of a toe with a constant of “1.” One added feature is that the toe constant compensates for mouths that are wider or narrower than the Normal Scale mouth of 1⁄4 of the circumference. For Flentrop this does not matter, because he used 1⁄4 mouths, but for a builder like Gottfried Silbermann who used 2⁄7 mouths, or Ernest M. Skinner who used 1⁄5 mouths, this compensation is critical, because wider mouths need more wind and narrower mouths need less. The toe constant allows us to compare the relative flow of wind in pipes with different diameters and different mouth widths. A good example in Figure 7 is the 8′ Roerfluit, which has slightly more wind than the 8′ Octaaf. Although it has a much smoother timbre, the 8′ Roerfluit’s slightly more powerful fundamental adds chorus depth to the much brighter 8′ Octaaf.
Toes control power, and in Flentrop organs designed for smaller acoustics I have found toe constants of 0.6 in the lowest mixture pitches, and this is a very restricted toe. A fully open toe has a toe constant of about 4, which we see in the highest pitches of the 2′ Octaaf and III Scherp in Figure 7.
Note the consistency of wind flow in the Flentrop principal chorus pipes at a given pitch, with a minimum flow of wind at about 1′ in pitch and much more flow in the bass and treble. This represents a voicing model for the Saint Mark’s acoustic. Similar patterns of wind flow exist in the 1692 Schnitger organ in the Hamburg Jacobikirche.14
The wind flow of the 4′ Speelfluit in Figure 7 is very instructive. Its lower cutups, relative to the 8′ Roerfluit, are explained by its more restricted toes. Closing the toe has the tonal effect of raising the cutup for a much warmer timbre at a lower power. The Speelfluit adds color to the more powerful Roerfluit, while restraining the power of the combined flutes as accompanimental stops.
Figure 8 data are estimated flueway depths based on observation of other work by Flentrop. In 1972 I did not have tapered wedges for measuring flueway depths. Wooden wedges are the safest material for documentation, but for a voicer, brass or steel wedges will last longer.15 The important feature of Flentrop flueways is that they are not used as a primary means of controlling power. Flentrop flueways do vary, but they vary within a restricted range at a given pitch. Neo-Baroque voicing emphasized a cutup recipe set to 1⁄4 of the mouth width with “open toes.” The result was that a voicer was often forced to use very narrow flueways to regulate both power and timbre, and the resulting sound was typically thin in fundamental warmth with a slow, gulping speech on the verge of overblowing. Flentrop used wind pressures and toes to control power, not the flueways, and he adjusted the cutup to achieve the desired timbres with fast speech.
In both modern and ancient work we will find an enormous variation in flueway depths. Although it is very rarely measured, flueway depth is of critical importance in understanding the different sounds of pipe organs. As the flueway deepens, more breathiness is heard in the sound. This is corrected by an increasing amount and boldness of nicking as the flueway depth increases. This is one of the reasons you will find many bold nicks in deep Romantic flueways. Flentrop’s voicing finds the flueway depth that will yield a tolerable breathiness with a minimum degree of nicking, and this is the optimum point for chiff. This is not a deep flueway, but it is much deeper than the razor-thin neo-Baroque flueways that resulted from arbitrarily low cutups. Both Andreas and Gottfried Silbermann used much deeper flueways than Flentrop, and their milder chiff is the result of their bolder nicking. Readers can find the flueway depths for some important historical styles in The Diapason.16
Figure 9 shows what happens when we divide the area of the pipe toe (the radius of the toe, squared, times π) by the area of the flueway it feeds (the flueway depth times the mouth width). In Figure 9 we see this data as a ratio of those areas. This tells us a great deal about the speech onset of the pipes. If the pipe toe is closed to the point where its area is less than the flueway area, the pressure will drop in both the foot and the flueway.17 We often see this in organs with higher wind pressures where the toes are strongly reduced to control power. In this situation, however, not only does the pressure drop at the flueway, the buildup of pressure in the foot is slower, and this can lead to slower speech. This form of slower speech is not immediately obvious, but a chorus with ratios above 1.0 will have a prompt attack, while pipes with ratios of 0.5 will have a noticeably slower attack, as is often heard in the smooth solo voice of the classical French cornet.18 When we look at theatre organs with extremely high wind pressures and deep Romantic flueways, we also find extremely small toes that produce ratios well below 0.5. This is why the attack of theatre organ flue pipes is much slower than what we hear in a Flentrop.
Ultra-low area ratios also explain in part why theatre organ pipes never have chiff. A fast rise in pressure in the foot and flueway is essential to the production of chiff, and we hear this when Biggs crisply opens the pallets on his 1958 Flentrop. Ratios close to 1 or above will be conducive to a fast pressure rise and the production of chiff, and in Figure 9 we can see that no Flentrop pipes have values below 1, and most pipes have values well above 1. This is a feature of Flentrop voicing in all of his organs for which I have data, and it is a significant factor in Flentrop’s fast, articulate voicing. Flentrop flueways are not deep in the Romantic style, and their areas are relatively small, with the result that even Flentrop’s more restricted toes still supply much more wind than the flueways need, and the fast pressure rise produces chiff.
Chiff can be eliminated in any ratio of toe and flueway areas by simply applying many bold nicks, but Flentrop used nicking sparingly, and when it is used, it is typically very fine in nature. Hook voicing also features relatively high area ratios, but the voicers used many bold nicks on every pipe, and no chiff is audible in their voicing. Theatre organs combine ultra-low area ratios with very bold nicking and unsurprisingly never exhibit chiff.
Figure 10 shows the mouth of a Flentrop pipe from about 1980, which is articulate, even with its two bolder nicks. The finest nicking in the center of the languid is more typical of the Saint Mark’s organ. Note that the flueway, while not deeply open in the Romantic style, is much deeper than typical neo- Baroque voicing.
The Pedaal
Figure 11 shows the diameter scales of the Pedaal. The scales of the larger pipes are consistent with the Flentrop model in Figure 3, and the diameters of the larger pipes were measured at the bottom. The Mixtuur is also consistent with the model notes. Like the Hoofdwerk, the flutes trend much wider as the pitch ascends.
The wind pressure of the Hoofdwerk is 80 millimeters, which is interestingly the same pressure found in the restored 1692 Hamburg Jacobikirche Schnitger. All other divisions at Saint Mark’s are winded on a very modest 68 millimeters of pressure, including the Pedaal. Flentrop once commented that wind pressure in a pipe organ is analogous to the tension of strings on a violin, with similar effects in the sound.
When I visited in 1972, the 32′ Prestant featured large ears at the sides of the mouths, and a few years later I observed that large wooden rollers had been added between the ears. This was perhaps an effort to make the 32′ sound more audible, as human hearing is very poor in the deep bass. At about 20 cycles per second we feel sound as much as we hear it, and a 32′ pipe resonates at 16 cycles per second. The addition of the rollers increases audible harmonic power to the sound, just as they add harmonic power to very narrow string pipes. Joseph Gabler found an elegant solution to this problem in his organ of 1750 at Weingarten: drawing the 32′ stop also draws the 16′ stop at the same time, making the sound both felt and more easily heard.
Tin was very expensive when Saint Mark’s Flentrop was constructed, the result of a powerful tin mining cartel. Many Flentrop organs utilized copper for larger façade pipes during this time as an alternative to zinc. The colorful patina on Flentrop copper pipes exhibits reddish earth tones and subtle greens. I asked Flentrop how he achieved this, and he laughed. The process was the result of long experimentation, and it involved strongly heating the pipes and applying the urine of cows to the heated metal. Flentrop smiled when he said that the smell in the shop was not at all pleasant. The lovely pastel colors of those copper pipes enhance the deep reds of the mahogany used in the casework, which Flentrop carefully selected from his supplier in Africa.
The full principal chorus of Flentrop’s magnum opus in its 1981 configuration is electrifying in the Praeludium in E Major by Vincent Lübeck <Soundclip 4>. The organ today features some wonderful additions by the shop of Paul Fritts.19
Paul Fritts and Company Organ Builders
Additions and changes to pipe organs can result in irreparable harm to the original sound. The additions and changes by the Fritts shop, however, are sympathetic to Flentrop’s original concept. They are exceedingly well executed, and Flentrop’s original voicing was left unchanged.20
In 1991 the console action was replaced with a suspended action. Germanic reeds were added at 16′ and 8′ to the Hoofdwerk, and the horizontal reeds were replaced at their original pitches with designs based on the 1762 work of the Iberian organbuilder Jordi Bosch. The original Flentrop reeds have been carefully packed and stored. The addition of a 32′ Pedaal Bazuin on the back wall to the rear of the Pedaal casework is a welcome one in a room whose large windows consume a great deal of bass sound. These alterations will hopefully diminish future appetites for changes to Flentrop’s historic magnum opus.
The precarious life of historic sounds
D. A. Flentrop’s organs are probably a very good representation of the sound of Arp Schnitger, which has very rarely if ever survived in its original form. Between 1953 and 1955 Flentrop undertook a major restoration of the 1720 Schnitger organ at Saint Michael’s Kerk in Zwolle to return it to its original condition, and Biggs recorded that magnificent sound in the 1960s.21 History teaches us that original sounds only survive in the very rarest of circumstances, and these are often found in depressed economies where there is no funding for restorations. Historically important sounds quickly disappear with the good intentions of restorers who change wind pressures, temperaments, pitch, and voicing to suit their own ears.22 This is why early documentation is so important, and it can expose later changes.
This article features a sample of scaling and voicing data from D. A. Flentrop’s magnum opus taken in its original form in 1972.23 It has hopefully provided readers with a better appreciation of the sound of D. A. Flentrop. Astute readers will also no doubt notice that fifty-one years elapsed before I carefully analyzed this data. I should have done this long ago. Tempus fugit, carpe diem.
Notes and references
All images are found in the collection of the author unless otherwise noted.
1. Barbara Owen, E. Power Biggs: Concert Organist (Bloomington, Indiana: Indiana University Press, 1987), pages 128–133.
2. wikiwand.com/en/Dirk_Andries_Flentrop, accessed July 6, 2023. From their reference: Kerala J. Snyder (Spring 2005), Symposium in Honor of Dirk A. Flentrop, Resonance.
3. Michael McNeil, “The Sound of Gottfried Silbermann,” Part 2, The Diapason, January 2023, pages 13–19.
4. Michael McNeil, “1863 E. & G. G. Hook, Opus 322, Church of the Immaculate Conception, Boston, Massachusetts,” The Diapason, Part 1, July 2017, pages 17–19, and Part 2, August 2017, pages 18–21.
5. McNeil, “The Sound of Gottfried Silbermann,” Part 2.
6. McNeil, “The Sound of Gottfried Silbermann,” Part 2.
7. Michael McNeil, “Designing an Historic Reed,” The Diapason, June 2023, pages 14–20.
8. saintmarks.org/music-arts/organs/the-flentrop-organ/ accessed July 12, 2023.
9. “Plainly audible” reverberation is measured at about -26 dB. The -60 dB architectural standard does not take into account the audibility of reverberation in the context of music, and it is also a source of grave disappointment for musicians and organbuilders. The standard needs to be revised for music.
10. Michael McNeil, “1863 E. & G. G. Hook Opus 322: Church of the Immaculate Conception, Boston, Massachusetts,” Part 1, The Diapason, July 2017, page 18.
11. Email the author for Excel files with the Saint Mark’s Flentrop data and/or the Jacobikirche Schnitger data at no charge at: mcneilmichael83@gmail.com. The Schnitger data is derived and graphed from: Heimo Reinitzer, Die Arp Schnitger-Orgel der Hauptkirche St. Jacobi in Hamburg (Hamburg: Christians Verlag, 1995), with restoration by Jürgen Ahrend and data measurements by Cor Edskes.
12. Ibid.
13. McNeil, “The Sound of Gottfried Silbermann,” Part 2; McNeil, “1863 E. & G. G. Hook, Opus 322, Church of the Immaculate Conception, Boston, Massachusetts,” Part 1.
14. Email the author for Excel files with the Saint Mark’s Flentrop data and/or the Jakobikirche Schnitger data at no charge at: mcneilmichael83@gmail.com
15. Michael McNeil, “The Sound of Gottfried Silbermann,” Part 2, The Diapason, January 2023, see Figure 15 on page 14 for an illustration of a wedge for measuring flueway depth.
16. McNeil, “The Sound of Gottfried Silbermann,” Part 2.
17. Email the author for Excel files with the Saint Mark’s Flentrop data and/or the Jacobikirche Schnitger data at no charge at: mcneilmichael83@gmail.com. The Schnitger data is derived and graphed from: Heimo Reinitzer, Die Arp Schnitger-Orgel der Hauptkirche St. Jacobi in Hamburg, (Hamburg: Christians Verlag, 1995), with restoration by Jürgen Ahrend and data measurements by Cor Edskes.
18. McNeil, “The Sound of Gottfried Silbermann,” Part 2.
19. saintmarks.org/music-arts/organs/the-flentrop-organ/.
20. saintmarks.org/music-arts/organs/the-flentrop-organ/.
21. E. Power Biggs, The Organ in Sight and Sound, Columbia Masterworks, KS 7263, ca. 1969. Many examples of Schnitger organs are included in this landmark recording. D. A. Flentrop wrote a primer on classical organ design for the twenty-eight-page book included with this vinyl recording.
22. Flentrop was right when he remarked that I would use my observations of his work to find my own sound. The temptation to modify organs to the taste of the restorer is very strong, and I have regrettably succumbed to that temptation, too. I carefully documented a Wm. A. Johnson organ and described the changes I made to it in these articles, “The 1864 William A. Johnson Opus 161: Piru Community United Methodist Church, Piru, California,” The Diapason, Part 1, August 2018, pages 16–20; Part 2, September, 2018, pages 20–25; Part 3, October, 2018, pages 26–28; and Part 4, November 2018, pages 20–24.
23. Email the author for Excel files with the Saint Mark’s Flentrop data and/or the Jakobikirche Schnitger data at no charge at: mcneilmichael83@gmail.com.
Sound clips
1. [00:34] Johann Sebastian Bach, Prelude and Fugue in A Minor, BWV 543, E. Power Biggs, Bach, the Great Preludes and Fugues, Volume 2, CBS Records, 42648, recorded in 1964 at the Busch Reisinger Museum, Harvard University, Cambridge, Massachusetts.
2. [00:30] Charles-Marie Widor, “Andante cantabile,” from Symphonie IV, opus 13, number 4 (1872), James Welch, Magnum Opus, Volume 2, Wilson Audiophile, WCD-8314, recorded in 1981 at Saint Mark’s Cathedral, Seattle, Washington.
3. [01:01] Carl Philipp Emanuel Bach (often attributed to Johann Sebastian Bach, BWV 565), Toccata and Fugue in D Minor, James Welch, Magnum Opus, Volume 1, Wilson Audiophile, WCD-8111, recorded in 1981 at Saint Mark’s Cathedral, Seattle, Washington. Exhaustive research by Michael Gailit has convincingly shown C. P. E. Bach as the most likely composer of this work. See “Exploring the unknown of BWV 565,” The Diapason, Part 1, June 2021, pages 18–19; Part 2, July 2021, pages 12–14; Part 3, December 2021, pages 16–18; Part 4, August 2022, pages 15–17; Part 5, September 2022, pages 19–21; and Part 6, October 2022, pages 15–17.
4. [00:40] Vincent Lübeck, Praeludium in E Major, James Welch, Magnum Opus, Volume 2, Wilson Audiophile, WCD-8314, recorded in 1981 at Saint Mark’s Cathedral, Seattle, Washington.
—It is strongly recommended to use Sony MDR 7506 headphones for the sound clips. Earbuds will not generate bass sound.
Saint Mark’s Episcopal Cathedral website: saintmarks.org.
Flentrop Orgelbouw website: flentrop.nl.