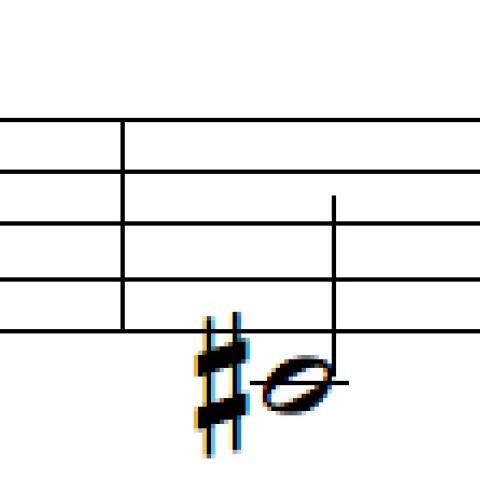Proportional relationships in Bach’s Die Kunst der Fuge and the intended duration of Contrapunctus XIV

“The governing idea of the work . . . was an exploration in depth of the contrapuntal possibilities inherent in a single musical subject.”¹ So says Bach scholar Christoph Wolff of Johann Sebastian Bach’s Die Kunst der Fuge, BWV 1080. Comprising fourteen fugues and four canons, we have inherited the work in an incomplete state; soon after Bach introduces his own musical signature as Contrapunctus XIV’s third subject and combines it with two previous themes, the music abruptly stops. There is no consensus on whether the ending was lost or simply never written; what is clear is that Contrapunctus XIV is notably missing Die Kunst der Fuge theme that unifies every other movement. In the 1870s, Gustav Nottebohm discovered that Die Kunst der Fuge theme could be combined with Contrapunctus XIV’s three preexisting themes to create a quadruple fugue.² It would then seem that this was Bach’s plan.

Because of abundant structures and patterns that Bach establishes in the existing part of the work, many aspects of Bach’s plans for the conclusion of Contrapunctus XIV can be estimated with varying degrees of confidence. Indeed, it seems likely that Bach had such remarkable compositional facility that he chose to limit himself with certain external and artificial restraints, such as the use of numerology. This is especially likely in such an abstract work, which is not guided by a text or any other limitation except conservativeness of musical material. These patterns and designs mean that ascertaining Bach’s intentions concerning the conclusion of Contrapunctus XIV requires much less guesswork and subjectivity than one might think.

One of the areas that is elucidated by the study of patterns and precedent is the intended length of Contrapunctus XIV. As we will see, Bach meticulously plans the lengths, subdivisions, and proportions of the polythematic fugues in Die Kunst der Fuge. When considering whether any proportional relationships exist in the work that could indicate how much longer Contrapunctus XIV should be, it seems most logical to start by examining the two triple fugues, Contrapuncti VIII and XI. This is because the forms of the polythematic fugues are mainly governed by the introduction and combination of themes. Contrapuncti VIII and XI are especially significant because as triple fugues they have more themes and sections, and therefore more in common with Contrapunctus XIV.

First, it is necessary to establish a methodology. The lengths of sections can be quantified by beats alone as well as by measures. (When counting beats, I always count quarter notes even if the movement is in cut time.) It is important to accurately calculate the exact number of beats in a section, as opposed to rounding to the nearest whole measure. This is not to say that Bach never rounds, but merely that exactitude can yield important insights.³ The lengths of sections can often be significant in and of themselves, and furthermore, once they have been accurately calculated, there are numerous relationships that can exist between sections.

The tools that seem most likely to be revealing are those of division and subtraction: to divide the lengths of sections by each other (larger by smaller or smaller by larger), or to subtract a shorter section from a longer one. We will find that many of these relationships have numerological significance that indicate intentionality behind their proportional designs.

Numerology and gematria

According to Encyclopedia Britannica, gematria is “the substitution of numbers for letters of the Hebrew alphabet, a favourite method of exegesis used by medieval Kabbalists to derive mystical insights into sacred writings or obtain new interpretations of the texts.”⁴ This concept is naturally not limited to Hebrew, although it is more easily applied to other alphabetic languages (i.e., letters represent sounds) than those that use syllabic (i.e., characters represent syllables or moras, e.g., Japanese) or logographic (i.e., characters represent words, e.g., Chinese) writing systems. Gematria and numerology are closely related, but not synonymous. All gematria might be called a subset of numerology, but not all numerology constitutes gematria. Specifically, gematria is a compartment of numerology based on assigning numerical values to letters to encode meaning.

In Appendix 1 of her book Bach and the Riddle of the Number Alphabet, Ruth Tatlow lists 33 different number alphabets. For the purposes of Bach study, the most common number alphabet is what Tatlow calls “Latin natural-order: variant 1,” shown in Figure 1.⁵

The concept behind this number alphabet is simple, but there are two important details to note: the omission of the letters “J” and “V.” Consequently, this number alphabet goes up to 24, not 26. This is particularly significant when Bach’s gematric designs incorporate his first initial, which notably is missing from this alphabet. Up until the eighteenth century, the Roman letter “I” was used to represent both the vowel sound normally associated with that vowel as well as the sound associated with the consonant “J.” Likewise, “U” stood in for “W.”⁶

This avenue of exploration in Bach’s music came to prominence in 1947 with the publication of four volumes about Bach’s cantatas by Friedrich Smend. One of Smend’s primary observations is the prominence of the number 14, now commonly associated with Bach.⁷ This number’s significance is derived from its gematric value (Figure 2).

In her book Bach’s Numbers, Ruth Tatlow points out the astonishingly serendipitous detail that the numbers corresponding to B, A, C, and H (2, 1, 3, and 8) also correspond to Bach’s birthday, March 21, 1685. Bach would have numbered dates in the order day, month, year, so his birthday would have been numerically represented as 21-3-85, if one omits the first two digits of the year.⁸ (The concluding “5” is not a part of the numerical parallel between Bach’s name and birthday.) Another number of great importance to Bach is 41: the retrograde of 14 and the sum of the letters J, S, B, A, C, and H (Figure 3). The last gematric sum of significance in this study is 55: the sum of 14 and 41. The sum of the digits one and four is also five, so another conception is that 55 represents the sums of the constituent digits of 14 and 41, placed side by side.

These three numbers appear frequently in Bach’s oeuvre. While it is outside the scope of this disquisition to catalog such instances in Bach’s broader output,⁹ it is worth noting certain appearances of these numbers in Die Kunst der Fuge. The following is a non-comprehensive list, most of which are cited from Indra Hughes’s dissertation:

• There are 14 contrapuncti. Additionally, a preliminary version of Die Kunst der Fuge, dating from the early 1740s, had 14 total movements.

• Bach likely intended to submit the work to Lorenz Christoph Mizler’s Correspondierende Societät der musicalischen Wissenschaften, an epistolary forum for the advancement of music theory. Bach waited to be admitted into this society until he would be its 14th member and commissioned the famous Hausmann portrait to commemorate his admittance—a portrait in which Bach is holding the last of his 14 Goldberg canons.¹⁰

• The first two notes of Die Kunst der Fuge theme, D and A, gematrically correspond to the numbers 4 and 1.11 The same can also be said of the first two and last two notes of Contrapunctus XIV’s first subject.

• The gematric sum of the notes comprising the original twelve-note version of Die Kunst der Fuge theme is 55. (D + A + F + D + C + D + E + F + G + F + E + D = 4 + 1 + 6 + 4 + 3 + 4 + 5 + 6 + 7 + 6 + 5 + 4 = 55)

• Contrapunctus II has 14 subject entries.¹²

• Starting in Contrapunctus V, the regular form of Die Kunst der Fuge subject has 14 notes, due to the addition of two passing tones.¹³

• The B-A-C-H motive appears in measures 40–41 of Contrapunctus V (Example 1).¹⁴

• Contrapunctus VI has 14 inverted entries.¹⁵

• Between the two double fugues (Contrapuncti IX and X), there are 14 double combinations.

• The B-A-C-H motive occurs in the alto and soprano voices of measures 40–41 of Contrapunctus X (Example 2).

• Section 1 of Contrapunctus XIV is 114-1⁄4 measures long, a mixed number with numerous allusions to 14 and 41.

• Contrapunctus XIV’s second subject has 41 notes.¹⁶

• The B-A-C-H motive is finally plainly revealed in the 14th fugue.¹⁷

• One additional gematric detail is worth consideration, although it does not use the numbers 14, 41, or 55. Bach titled the work Die Kunst der Fuga, somewhat peculiarly eschewing the German “fuge” in favor of the Italian “fuga.” Anatoly Milka has theorized a numerological explanation for this choice: the gematric sum of the letters in “Johann Sebastian Bach” is 158, which is equal to the gematric sum of the letters in “Die Kunst der Fuga.” If, however, Bach had retained the German “fuge,” the gematric sum of the work’s title would have been 162, and would therefore not have matched the gematric sum of his full name. Additionally, the sum of the numbers 1, 5, and 8 is 14.¹⁸

There are also those who cite certain gematric elements of the final measure as evidence that Bach intentionally left the work incomplete. First, the digits of the final measure—2, 3, and 9—add up to 14. Importantly, this is also the exact number of measures in the Canonic Variations on “Vom Himmel hoch da komm’ ich her,” BWV 769, for organ, another work dating from the late 1740s that Bach submitted to Mizler’s Correspondierende Societät der musicalischen Wissenschaften. Additionally, 2 + 39 = 41 and 23 – 9 = 14.

The remaining gematric details are more easily seen in the autograph, shown in Figure 4. (Note that the top staff is in soprano clef.)

• The final complete measure (measure 238) has 14 notes.

• The final two bass notes are A and D, whose gematric equivalents are 1 and 4.¹⁹ (These notes are enclosed in a black box.)

• The final harmony consists of two Ds and an F. When these pitches are converted into numbers, D is 4 and F is 6, making the gematric sum of this chord’s notes 14 (4 + 4 + 6 = 14). (These notes are enclosed in a red box.)

• In the final measure, seven of the tenor’s eight notes are on the top staff. Only the antepenultimate note, a lone A, is transferred to the bottom staff. The result is that the only two notes in the bottom staff of the last measure are D and A, whose gematric equivalents are 4 and 1.²⁰ Bach’s decision to put the A on the lower staff seems fussy unless it was done to create a gematrically significant design. (These notes are enclosed in a blue box.)

Contrapunctus VIII

Returning to the subject of proportion, let us begin with Contrapunctus VIII—a three-voice triple fugue. In Die Kunst der Fuge’s polythematic movements (i.e., Contrapuncti VIII through XI), new sections are generally delineated through the introduction of new themes. Contrapunctus VIII, however, has one additional section because Bach delays combining all three themes. All three themes are in play in Section 3 but are not presented in triple combination until Section 4. Following that model, Section 1 begins with the introduction of Theme 1 in measure 1 (Example 3), a new theme to the work that gradually descends by one octave over the course of four measures. As previously mentioned, it is important to note that Contrapunctus VIII begins with a half rest, so Section 1 does not begin until the third quarter of measure 1.

Section 2 begins on beat three of measure 39 with the introduction of Theme 2, an inverted form of B-A-C-H utilizing a repeated-note motive, in immediate combination with Theme 1 (Example 4).

Finally, Section 3 begins on beat two of measure 94, where a new form of Die Kunst der Fuge theme, characterized by downbeat quarter rests and composed mainly of quarter notes, enters.²¹ Finally, Section 4 begins on beat three of measure 147 with the first of five triple combinations. Section 1 is 38 measures or 152 beats, Section 2 is 54.75 measures or 219 beats, Section 3 is 53.25 measures or 213 beats, and Section 4 is 41 measures or 164 beats. For ease of reference, Table 1 outlines Contrapunctus VIII’s four sections.

From the chart, one can see that there is a general arch form; the two inner sections are larger than the outer two, the inner sections are almost the same length, and the outer sections are also close in length.

Keeping in mind that the most significant numbers in Die Kunst der Fuge are 14 (the sum of the letters
B + A + C + H), 41 (the sum of the letters J + S + B + A + C + H and the retrograde of the number 14), and 55 (the sum of 14 and 41), these are the numbers that would most clearly indicate intentionality in Bach’s proportional scheme. For this reason, the first step is to look for those numbers (14, 41, and 55) in Table 1. Instantly, one can see that Section 4 is exactly 41 measures. Slightly less obvious is the fact that Section 2 is almost exactly 55 bars. Another potentially significant detail is that the first triple combination occurs in measure 147—a measure beginning with the number 14 and whose latter number is half of 14. Moreover, Section 2 is exactly 55 beats longer than Section 4, and Section 3 is 213 beats long, corresponding to the letters B - A - C.

Finally, and most importantly, sections 2 and 3 are both almost exactly 1.4 times longer than Section 1. Section 3 is slightly closer to this proportion (213 / 152 ≈ 1.4013 . . .) than Section 2 (219 / 152 ≈ 1.4407 . . .). Even more incredible, the proportion between sections 1 and 2 can be rounded to 1.441, thereby combining the numbers 14 and 41! While such a specific number may sound far-fetched, this will not be the last time we see this level of detail, or indeed this exact proportion.²²

Contrapunctus XI

We now turn to Contrapunctus XI—the most adventurous and dramatic movement of the work. Contrapunctus XI is a four-voice triple fugue with an additional chromatic countersubject. It is the sister to Contrapunctus VIII in that they use the same three subjects, but Contrapunctus XI inverts them or, depending on how one looks at it, uninverts them, since Contrapunctus VIII uses the inverted forms of Die Kunst der Fuge and B-A-C-H themes and Contrapunctus XI uses the rectus forms. In the ilk of Charles Ives’s cumulative form technique, in which Ives reversed the standard model of exposition and development by beginning with fragments and motives from a theme that culminates in a plain statement of the entire theme near the end of the piece,23 it is not until Contrapunctus XI that one hears these themes turned right side up (rectus), enabling one to more easily recognize them for what they are (particularly the B-A-C-H theme, which is still masked by the addition of repeated notes in Contrapunctus XI).²⁴

Contrapunctus XI is also, from a formal and proportional perspective, the most enigmatic movement because of the presence of multiple extra sections (i.e., there are more sections than there are themes). Section 1 begins on beat two of measure 1 and introduces Theme 1, the rectus form of the rhythmically altered Die Kunst der Fuge theme from Contrapunctus VIII. Section 2 uninverts Contrapunctus VIII’s first theme and introduces a prominent chromatic countersubject (Example 5).

Section 3 unexpectedly eschews all previously introduced material and simply exposes the inverted form of Theme 1 (i.e., Die Kunst der Fuge theme). Section 4 introduces the rectus form of the B-A-C-H theme in immediate combination with Theme 2. Finally, Section 5 uses all three themes and presents three triple combinations. Table 2 outlines these sections and their respective lengths.

From this table, one can make a number of crucial observations. First, Section 1 is exactly three fifths as long as Section 2 (175 x .6 = 105), a reference to the three themes and five sections, perhaps? Second, Section 3 is .417 times longer than Section 2.²⁵ Third, Section 5 begins in measure 146 (which begins with the number 14). Fourth, Section 4 is 1.46 times longer than Section 5, meaning sections 2 and 3 have the same proportional relationship as sections 4 and 5. Finally, Section 1 is 1.438 times as long as Section 3.

At this point, all the musical evidence indicates that Bach not only meticulously controlled the proportional scheme of Contrapunctus XI but went to extraordinary lengths to use proportions and durations of numerological significance. Yet there are even more astonishing features of this movement’s proportions. First, it is worth noting the relative lengths of the different sections—specifically, that there are two overlapping arches. Sections 1 through 3 form an arch of smaller-larger-smaller, and sections 3 through 5 also form an arch of smaller-larger-smaller.

The most notable feature of this movement’s proportions reveals itself when one adds together the two smaller sections in each arch. Section 1’s 105 beats plus Section 3’s 73 beats add up to 178 beats, which is very close to Section 2’s 175 beats. This on its own may just be coincidence, but an examination of the second arch (sections 3, 4, and 5) demonstrates that it is almost certainly not, since the second arch has the same property; Section 3’s 73 beats plus Section 5’s 155 beats add up to 228 beats, which is even closer to Section 4’s 227 beats.

The numbers are even more exact if one adds measures instead of beats: Section 1’s 26.25 measures + Section 3’s 18.25 measures = 44.5, compared to Section 2’s 43.75 measures. And for sections 3 through 5, Section 3’s 18.25 bars + Section 5’s 38.75 bars = 57—extremely close to Section 4’s 56.75 measures. (This is part of the reason for measuring durations in both beats and measures; what may seem somewhat inexact when measured in beats can seem much more precise when measured in measures, particularly when rounding.)

To put this in simpler terms, Section 1 + Section 3 = Section 2, and Section 3 + Section 5 = Section 4! It is much like the Fibonacci Sequence (1, 1, 2, 3, 5, 8, 13, . . .),
which adds together the previous two numbers in the sequence to produce the next number, except these numbers are out of order. (In this case, one adds outer numbers to produce the inner number, so the first and third numbers add up to the second, the third and fifth numbers add up to the fourth, etc.)²⁶

The enigma of Contrapunctus XI is Section 3. Why does Bach eschew all other themes and compose a section just for the inverted form of Theme I? After all, Theme I occurs in inversion only twice more, so it is not a particularly important thematic variant in this movement. Additionally, themes are typically treated cumulatively; Bach does not usually eschew a previously stated theme in favor of a different previously stated theme. (An example would be introducing Theme 2 and then reverting to using only Theme 1.) He will often temporarily abandon a previously established theme to introduce a new theme, but to do so for an old theme is regressive. (A typical example of the former is in Contrapunctus VIII, where Themes 1 and 2 drop out upon Theme 3’s entry but return later in combinations with Theme 3.) There are a couple exceptions in which Bach does backslide to a previous theme, but these are, without exception, because of permutational designs.

Furthermore, this section is rhythmically calmer than the surrounding sections; sections 2, 4, and 5 have fairly constant eighth-note motion, while Section 3 has more quarter-note motion. Bach has clearly assigned this section a special role. If Bach had a specific reason for doing so, one possibility is because Section 3 is the central section and links the two arches (sections 1 through 3 and sections 3 through 5). Additionally, he needed a way to clearly articulate five sections in this movement—two more than would be necessary in a triple fugue. Perhaps this was his way of accomplishing that.

So what do these analyses tell us about Bach’s intentions concerning Contrapunctus XIV? First, they demonstrate a high degree of care and intentionality in the proportional schemes of both triple fugues. For better or for worse, another key takeaway is that Bach’s proportional structures are inconsistent from movement to movement. Contrapunctus VIII is a three-voice triple fugue that has four sections that form an arch (shorter outer sections and longer inner sections), and Contrapunctus XI is a four-voice triple fugue that has five sections that can be organized into two arches.

The features that are consistent, and which will likely apply to Contrapunctus XIV, are a meticulously planned proportional design and the prevalence of the numbers 14, 41, and 55. Next, we will examine the extant part of Contrapunctus XIV to hopefully find the beginnings of a proportional structure that will shed light on the length of the movement and the sections it comprises.

Contrapunctus XIV

The challenge in an examination of the proportional relationships in Contrapunctus XIV is, of course, that the movement is incomplete. Sections 1 and 2 are complete, Section 3 is partially written, and Section 4 is missing completely. Since it takes three objects to establish a pattern (and we have only two objects in their entirety), any theories regarding Bach’s intended proportions cannot be positively proven; we do not have all the necessary information. The other complication is that if a study of the proportional relationships in Contrapuncti VIII through XI reveals anything, it is that Bach is not so simple-minded as to repeat proportional schemes between movements. This means that the principles we derived from previous proportional evolution can only broadly guide a completion of Contrapunctus XIV. What does seem likely to remain true, however, is that the numbers 14, 41, and 55 will guide the proportional schemes. Indeed, even the number of this contrapunctus appears to carry meaning.

Given that Contrapunctus XIV was clearly intended as a quadruple fugue (as proven by Gustav Nottebohm),²⁷ the most obvious division of sections would be one section per theme. (This is the same model that Bach used in Contrapunctus IX, albeit on a much smaller scale.) This would mean that Section 1 is dedicated to Theme 1, Section 2 uses themes 1 and 2, Section 3 uses themes 1, 2, and 3, and finally, Section 4 uses all four subjects—a straightforward, cumulative design.

The extant part of Contrapunctus XIV provides support for this hypothesis. In Contrapunctus XIV, the themes are treated cumulatively. Section 2 introduces Theme 2 while retaining Theme 1, eventually combining them. Section 3 introduces Theme 3 while retaining themes 1 and 2, eventually combining all three (Example 6). This is not so in Contrapuncti VIII or XI. In Contrapunctus VIII, Bach introduces Theme 3 in Section 3 but starts a new section (Section 4) to present triple combinations. Contrapunctus XI is even less straightforward; Theme 1 disappears in Section 2, and then Theme 2 disappears in Section 3. Section 4 finally uses all three themes, but not in triple combination until Section 5. The extant part of Contrapunctus XIV clearly shows a more direct approach to the exposition and combination of themes.

Now that we have established the likelihood that Bach intended Contrapunctus XIV to have a one-to-one ratio of subjects to sections, let us examine the durations and proportions of the surviving parts. The gigantic first section begins on beat three of measure 1 and goes to the downbeat of measure 115, giving it a duration of 457 beats or 114.25 measures. It seems highly serendipitous that the number of measures in Section 1 can be conveyed as 114-1⁄4—a number with numerous allusions to 14 and 41 (yet another reason to measure durations in both beats and measures). Section 2 is in a Stile antico idiom and is composed largely of quarter-note motion. Theme 1 comprises seven notes and has the interesting quality of being a melodic palindrome. (See Example 7.)

Importantly, Section 2 overlaps with Section 1 by four beats because Theme 2 enters before the other voices have completed their cadence marking the end of Section 1. Theme 2 is composed mainly of eighth-note motion and is exactly 41 notes. The increased rhythmic activity of Section 2 breaks the retrospective style of Section 1. Theme 2 is also the only theme in Contrapunctus XIV that is not presented in inversion in the extant sections (excluding Theme 4, which has not yet occurred in any version). Section 2 begins with the introduction of Theme 2 in the alto on beat two of measure 114 (another reference to 14) and continues through beat two of measure 193, making Section 2 317 beats or 79.25 measures. (See Example 8.)

Section 3 begins on beat three of measure 193 and trails off in measure 239.28 This gives the extant part of Section 3 a length of 186 beats or 46.5 measures, although these numbers may not be particularly significant as they represent only part of a section. Stylistically, Section 3 brings about another shift; the counterpoint becomes rhythmically less active, and the harmony becomes markedly more chromatic and adventurous.29 (This is partially by virtue of Subject 3’s chromatic profile and longer note values.) This marks the end of the extant part of Contrapunctus XIV. (See Table 3.)

One of the challenges of deducing Bach’s intentions is that with only two complete sections, there is not enough information to establish a pattern per se. Nevertheless, it seems likely that the sections should get shorter. As previously stated, Section 1 is truly massive; it has more measures than every movement of the work except the four polythematic fugues and takes about four minutes to perform on its own. The movement would likely feel bloated and disbalanced if there were another section even longer than this one, and indeed, Section 2 is about 30 measures shorter. A final, more subjective reason to believe that the sections will continue getting shorter is that Section 3 is clearly intensifying in both rhythmic and harmonic activity. In just 46.5 bars, it is already clearly approaching a climactic point, at which time Theme 4 will likely enter.

Bach scholar Dr. Gregory Butler of the University of British Columbia at one point theorized that each section of Contrapunctus XIV is intended to be approximately two thirds the length of the preceding section.30 He explains:

As it appears in the print in its incomplete state, this work occupies five pages. It seems clear that the finished version would have fit nicely on six pages. If we examine the relative proportions of the three extant sections of this fugue, we notice a consistent diminution in the lengths of successive sections. Moreover, section 2 (78 measures) is almost exactly two-thirds the length of section 1 (115 measures), and section 3, not quite complete, occupies forty-six measures and conceivably in its complete state would have occupied approximately two-thirds the length of section 2 (52 measures). Adhering to the same proportions, section 4 may well have occupied approximately two-thirds the length of section 3, that is, approximately thirty-four measures. This would leave approximately forty-six measures for the concluding sixth page which is exactly the average number of measures per page for the first five pages as they appear presently in the print.³¹

This theory has a number of issues. The reader may notice Butler’s use of language to indicate approximation. He rounds the sections to the nearest whole measures, and his proportional theory also relies on rounding. Furthermore, he makes mathematical errors, claiming that two-thirds of 52 bars is 34 bars when it is actually closer to 35. He then says that Section 3 needs six more measures and that Section 4 should be 34 measures—a clear sum of 40 measures—but states that this fits “exactly” with one additional page of manuscript, equivalent to 46 measures.

If there is one conclusion to be made from our examination of the proportions in the triple fugues, it is that Bach’s proportional schemes are anything but approximate. Another reason to doubt Butler’s theory is that it does not leave enough time in Section 3 to include even one more triple combination, if there is to be any connecting episodic material. Indra Hughes, whose dissertation, “Accident or Design? New Theories on the Unfinished Contrapunctus 14 in J. S. Bach’s The Art of Fugue, BWV 1080,” is one of the major contributions to Die Kunst der Fuge research, agrees that Butler’s theory is not sufficiently precise and proposes a much more specific and convincing theory.³²

While it seems likely that Bach intended each section to be shorter than the preceding one, this is not proof of a more detailed proportional relationship. Hughes, however, has discovered a feature in the autograph that indicates that the exact lengths of sections were of great importance to Bach. This detail arises from an edit that Bach made at the end of Section 1. Bach crossed out the original material in measures 111 and 112 and replaced them with three measures, thereby adding a bar. The edit can be seen in Bach’s hand in Figure 5; the two measures at the top right have been crossed out and replaced with three measures of tablature in the bottom margin. The two versions are presented in a more readable fashion in Examples 9 and 10.

Hughes argues that there is not a substantial musical difference between the first and second versions, so therefore it is likely that the reason for the edit was for Bach to correct a proportional error, an error that could be fixed by adding one bar to Section 1. In rejection of strong musical reasons for the replacement, Hughes writes the following:

It seems a curious and puzzling change for Bach to have made, and it does not seem easy to find a musical reason for the rejection of the original bars 111 and 112. If Bach had not made the change, but had left the score with those two bars unaltered, would scholars and analysts today point to them and identify them as a weak moment? Perhaps it might be argued that the new bar 111 strengthens the approach to the following cadence (bars 113–114) by the move to the subdominant that was not present in the original; and it might be argued that the new bar 113 is rhythmically very slightly more interesting than the old bar 112. But these are tiny points of argument and I am convinced that if the change had not been made, nobody would ever have criticized the old bars 111 and 112 as being weak.³³

Hughes further refines Butler’s theory by more accurately calculating the lengths of sections. Butler calculated only whole measure numbers and did not account for overlapping sections, giving him durations of 115 measures and 78 measures for the first two sections, respectively.³⁴ Hughes calculates sections 1 and 2 as being 114.25 and 79.25 measures, respectively. This means that Section 1 is approximately 1.44 times longer than Section 235—our first evidence that Contrapunctus XIV’s proportional scheme is deliberate and numerologically determined.

Hughes’s argument gains traction when one uses this proportion to calculate the length of Section 3. Section 2’s 79.25 measures divided by the hypothesized ratio of 1.44 gives a quotient of 55 measures for Section 3—the section that introduces Bach’s name as the third subject.³⁶ Now there is very little doubt that these relationships are deliberate. This also conveniently leaves time for one more triple combination before Section 3 concludes.³⁷

Hughes then calculates that Section 4 should be 38 measures (although this is a rounded figure), reaching the conclusion that the total number of missing measures is 47. While I agree loosely with most of what Hughes postulates, there are a few fallacies and inconsistencies in his calculations that must be addressed. First, Hughes concludes that the correct proportion between sections is 1.44 but provides no reason for the presence of an additional “4” in the hundredths decimal place. (The reasons for this specific number will be discussed in greater detail later.)

Second, Hughes does a fair amount of rounding while criticizing others for doing so. An example of this is his calculation that Section 4 should be “exactly 38 bars long.”³⁸ In reality, this number is not so exact; it should actually be 38.194. Of course, some rounding is necessary, but rounding to 38.25 measures (38 measures and one beat) would be closer than rounding to 38 measures even. Rounding to the nearest beat instead of the nearest whole measure would dictate that the movement ends with a downbeat quarter note. (This is assuming that Section 4 cannot begin on beat three of a measure, since Die Kunst der Fuge theme would almost certainly enter on a downbeat.)

Of course, one could get around this by ending the work with a quarter-note—perhaps with a fermata. It is perhaps, however, not a stretch to suggest that Bach might have rounded this to 38 measures so that the work could end with a whole note. This is not a detail that should be taken lightly though; to round Section 4 to the nearest measure effectively excises a measure of music from the section and the entire movement. If Section 4 is rounded to 38 measures, then the final measure (measure 286) will most likely be a whole note. If, however, Section 4 is rounded to 38.25 measures, then the final measure (measure 287) would be a quarter note with a fermata (likely sounding the same as a whole note), thereby making measure 286 the penultimate measure and freeing it up for an additional measure of cadential material.

Finally, Hughes is generally quite meticulous about the lengths of sections—and this allows him to make important contributions to proportional theory—but he makes one significant error when he notes that Section 3 begins on beat three of a measure but forgets this detail when determining where Section 3 ends. In his calculations, he incorrectly starts Section 3 on the downbeat of measure 193 instead of beat three of measure 193. This leads him to believe that Section 3 needs an additional nine measures, instead of 8.5. Truthfully, at 55 measures, Section 3 must end on beat two of measure 248, a measure whose digits add up to 14.

This means that Section 4 must either start on beat three or overlap with Section 3 by two beats, but as previously stated, it seems unlikely that Die Kunst der Fuge theme would start on beat three, making the overlap the more likely choice. To account for this overlap, one must subtract two beats from the final calculation of the intended duration of Contrapunctus XIV. This puts Hughes’s calculation off by one whole measure: two beats off for starting Section 3 too early and two beats off for not overlapping sections 3 and 4. The question of whether one should round Section 4 to the nearest beat may also potentially push Hughes’s solution off by an additional beat. Table 4 compares Butler’s, Hughes’s, and my own theories and calculations.

As previously mentioned, the problem that Hughes faces is why the proportion is 1.44 instead of simply 1.4. He excuses this concern by pointing out that the proportional relationship is consistent, if not exact, and that there are other works by Bach with proportional relationships that are close to 1.4 but not exact.

Before exploring this issue further, it is vital to remember that Bach’s ways of solving mathematical problems would have been very different from our own. Doing these problems by hand, as Bach would have done, yields three very interesting (and I believe previously undiscovered) observations. The first and most obvious is that when 114.25 is converted into a mixed number, it is 114-1⁄4, a number with several allusions to 14 and 41.39 The second comes from the fact that Bach likely would have made these calculations in improper fractions (or beats) rather than decimals to facilitate division. To take the two complete extant sections as examples, Section 1’s 114.25 bars become 457/4, and Section 2’s 79.25 bars become 317/4. If one subtracts 317 from 457, the remainder is exactly 140, another evidently Bachian number. Since we are working with quarter measures in common time, Section 1 is exactly 140 beats longer than Section 2.

The final observation comes from dividing 457 by 317. The benefit to doing this division by hand is that the solution will not include a long string of decimals that a calculator displays. It is not surprising that the first three digits of the solution are 1.44, as Hughes claims. If, however, one solves to three decimals instead of two, then the third decimal is 1, producing a quotient of 1.441. At first glance, this new solution works much better than Hughes’s. While Hughes struggled to explain why his ratio is 1.44 instead of simply 1.4, this new proportion is both more specific and more numerologically significant, as it combines the numbers 14 and 41. Furthermore, it has precedent in the work; in Contrapunctus VIII, Section 2 is 1.441 times longer than Section 1.

To determine more certainly whether this proportion is more accurate, one must test whether the extra one thousandth consistently yields results that are closer to the actual number of measures present. To start, let us take 114.25 measures and divide it by Hughes’s 1.44. This gives us 79.340. (I will consistently round to the nearest thousandth.) If, however, we divide it by my 1.441, we get 79.285—a number that is not insubstantially closer to Section 2’s actual 79.25 measures. (See Table 5.) The extra one thousandth makes a surprisingly significant difference. If we take Section 2’s 79.25 bars and divide it by 1.44, we get 55.035. If we divide it by 1.441, though, we get 54.997. Once again, this solution is slightly closer to the hypothesized 55 bars in Section 2. (See Table 6.)

The final section, however, creates problems with either theory (1.44 or 1.441). When one divides Section 3’s 55 bars by 1.44, the solution is 38.194. When one divides it by 1.441, the quotient is 38.168. (See Table 7.)

Neither of these answers is very close to a round number of measures or beats, but the latter solution is slightly lower and therefore closer to a whole measure. This may tip the scale toward the argument that Bach intended for Section 4 to be 38 measures even—not, as previously considered, 38.25 measures (which would have required the last chord to be a quarter note with a fermata). Bach probably recognized that, at some point, some rounding would be necessary in his numerological games. Bach’s genius is, after all, still bound by the laws of mathematics.

When mapping out this movement, Bach may have begun with one of two conditions: that Section 2 would be 114-1⁄4 measures or, alternatively, that Section 3, the section in which he introduces his musical signature, would be 55 measures. These numbers are both, after all, significant to Bach. He must have been quite tickled to discover that 55 x 1.441 x 1.441 ≈ 114-1⁄4, but nevertheless, he must have started with one or the other—55 or 114-1⁄4. For this reason, it may be enlightening to compare Hughes’s and my proportional theories starting from both of those numbers. Table 8 compares the two theories starting with 114.25 measures in Section 1 as the reference point.⁴⁰ Table 9 compares the proportions between Hughes’s theory and my own using 55 measures in Section 3 as the reference point.

These tables show that, regardless of which reference point one starts from, 1.441 is a consistently more accurate proportion than 1.44. Table 8 also demonstrates something else that indicates why 1.441 is the more likely solution. When one looks at the column for Hughes’s proportion, one can see that his ratio consistently gives an answer that is slightly too high. The solutions produced by a ratio of 1.441, however, are slightly too high in the cases of sections 2 and 4, and slightly too low for Section 3. This means that no other proportion can truly be said to be closer. If one uses a number any higher than 1.441, Section 3 will be less accurate, and if one uses a number any lower than 1.441, sections 2 and 4 will be less accurate. When all the answers are too high though, as in Hughes’s ratio, it is clear that the proportion can be refined.

The extra beat

The remaining issue concerning the length of Contrapunctus XIV is the length of Section 4 and whether it should be rounded to the nearest measure or nearest beat. There are a number of factors that should at least be considered. First is the purely musical issue of ending an hour-and-a-half-long work. It would be unusual to end such a work with a quarter note, but having a fermata on the note would alleviate that to a degree; the difference would then arguably be only visual. As previously mentioned, using the proportion 1.441 instead of 1.44 pushes the length of Section 4 down by a little over three hundredths (38.1679 versus 38.194), but this is an admittedly minor difference.

It may once again be revealing to consider how Bach would have done his calculations. If one uses long division to calculate the length of Section 4, as Bach must have done, then he would not have seen a long string of decimals. He could have merely solved for the nearest whole number, in which case he would have reached 38 as a final answer and been done with it. But even if he continued to solve for the first decimal, he would have seen only a “1” in the tenths place, which he still would have likely been content to round down to zero. It is not until one solves for the hundredths place and gets 38.16 that this issue arises at all. It seems likely that Bach would not have been particularly bothered by this discrepancy, if indeed he was even aware of it.

In summary, I conclude that Section 3 requires another 8.5 bars—plus filling in the remaining voices of measure 239—and that Section 4 should be 38 measures, keeping in mind that it will overlap with Section 3’s last half measure. This gives one enough time to include one more triple combination in Section 3’s remaining 8.5 bars, as well as multiple quadruple combinations and episodes in Section 4. It is not, however, so long that the drama that has been reached by measure 239 will become an anticlimax. According to this theory, the movement should be 285 measures. This is calculated by adding the lengths of the sections (114.25 + 79.25 + 55 + 38 = 286.5) and subtracting one measure for the overlap of sections 1 and 2 and another two beats for the overlap of sections 3 and 4 (286.5 – 1.5 = 285). The durations and overlaps of the four sections can be seen in Figure 6.

Large-scale numerology

Finally, let us consider the sum total of all the movements. If one counts the lengths of the mirror fugues and their mirrors, thereby doubling the lengths of the mirror fugues to 254 measures, then the entire length of Die Kunst der Fuge is 2,135 measures. The realization that my proportional theory put the entire work at 2,135 measures immediately gave me pause. This is, after all, three short of the numbers which gematrically correspond to Bach’s name: 2,138. This caused me to wonder whether Bach was also intentional about the length of the entire work, which in turn led me to test what would happen if I aimed for a sum total of 2,138 measures by increasing Contrapunctus XIV to 288 measures, rather than 285. Obviously, the durations of sections 1 and 2 are fixed and cannot be tailored. Bach left Section 3 incomplete, but my proportional theory is largely based on the numerological significance of Section 3 being 55 bars. This leaves Section 4, which according to my original theory was 38 bars. Amazingly though, adding three measures increases it to exactly 41 measures. Through the addition of just three bars, the length of Section 4 and the length of the entire work suddenly achieve great gematric meaning. The question, as always, is: was this Bach’s intention?

The real issue here is whether Bach would sacrifice the integrity of his proportional scheme to inject the entire design with greater personal numerological significance. To better judge this, we must determine the degree to which this change would affect the proportional scheme. Before doing so, however, it is worth remembering that Section 4 was already problematic. When one divides 55 (the conjectured duration of Section 3) by 1.441, the quotient is approximately 38.168, which we rounded down to 38 (after first considering whether to round to 38.25, or 38 measures and one beat). This is significantly less precise than the proportions of the previous sections (72.285 versus the actual 72.25 measures in Section 2, and 54.997 versus the conjectured 55 bars in Section 3).

When one takes Section 3’s hypothesized 55 bars and divides them by 41 bars for Section 4, the proportion is approximately 1.341. This is not terribly far off from the originally theorized proportion of 1.441. Additionally, it still ends with the numerologically significant digits “41.” It is actually quite intriguing that the two numbers only differ by one digit.

The question remains: if Bach had realized that adding three measures to Section 4 would give both the section and the entire work gematrically significant durations, would it have been worth the small concession of modifying a proportional scheme that, at this point, was already falling short?

I believe the answer is yes; Bach would have succumbed to such a temptation. In fact, it must have been the design all along. It would be quite a coincidence for Bach to see the original proportional scheme of 1.441 through to the end and only then realize that the work was three bars short of 2,138 measures. Far more likely, he began by assigning 288 measures to Contrapunctus XIV so that the sum of the work’s movements would be 2,138. Knowing that the sections would diminish in length, he then assigned 41 measures to Section 4 and 55 measures to Section 3. At this point, he switched to a more exact proportional scheme of 1.441, making Section 2 79-1⁄4 measures and Section 1 114-1⁄4 measures, the latter of which—he must have been pleased to learn—is a number with about as many references to 14 and 41 as a five-digit number can have. The length of each section can be seen in Table 10.

These sections add up to 289.5 measures, but because of a one-measure overlap between sections 1 and 2 and a half-measure overlap between sections 3 and 4, the total duration of Contrapunctus XIV will be 288 measures. Since Bach’s final bar is measure 239, Contrapunctus XIV requires 49 more measures: 8.5 more measures in Section 3 and 41 measures for Section 4, with these two sections overlapping by two beats. (See Figure 7.)

It is my hope that this document may have use outside of the narrow scope of determining the intended duration of Contrapunctus XIV; more broadly, I hope to shed a bit more light on Bach and his compositional tendencies. The topic of proportion in Bach’s oeuvre is ripe for further examination, and we have only begun to scratch the surface. By now, there is no question that Bach was an enthusiastic practitioner of Augenmusik and hid all sorts of elaborate structures in his music. The question is: will we seek them out?

Notes

1. Christoph Wolff, Bach: The Learned Musician (New York: W. W. Norton, 2000), 433.

2. Gustav Nottebohm, “J. S. Bach’s letzte Fuge,” Musik-Welt, nos. 20 and 21 (1881): 2, http://ks4.imslp.net/files/imglnks/usimg/f/fc/IMSLP348435-PMLP562864-No….

3. Counting beats in large sections can be more complicated than one might expect, particularly if the passage includes partial measures. The formula for doing so is as follows: (last complete measure – first complete measure + 1) x 4 beats + any beats from surrounding partial measures. For example, if one wanted to count the beats from beat 2 of measure 4 to beat 2 of measure 36, then one would start with 35 (the last full measure) and subtract five (the first full measure) for an answer of 30. Then add one for a sum of 31 and multiply that by four beats for a product of 124. Then add the extra three beats of measure 4 and the extra two beats of measure 36 for an answer of 129 (124 + 3 + 2 = 129).

4. Encyclopædia Britannica, s.v. “Gematria.”

5. Ruth Tatlow, Bach and the Riddle of the Number Alphabet (Cambridge, England: Cambridge University Press, 1991), 133.

6. Indra Hughes, “Accident or Design? New Theories on the Unfinished Contrapunctus 14 in J. S. Bach’s The Art of Fugue, BWV 1080” (D.M.A. diss., University of Auckland, 2006), 3–4.

7. Ibid., 4.

8. Ruth Tatlow, Bach’s Numbers (Cambridge, England: Cambridge University Press, 2015), 70.

9. For perhaps the preeminent study of this field, see Ruth Tatlow’s Bach’s Numbers. The trajectory of Tatlow’s opinion on this topic is intriguing. In her 1991 book Bach and the Riddle of the Number Alphabet, she argues against most numerological and gematric interpretations of Bach’s music. Now, after something of a Damascene conversion, she is its leading exponent.

10. Hughes, “Accident or Design?,” 18.

11. Ibid.

12. Ibid.

13. Ibid.

14. Ibid.

15. Ibid, 19.

16. Ibid.

17. Ibid.

18. Anatoly P. Milka, Rethinking J. S. Bach’s Art of Fugue, trans. Marina Ritzarev, ed. Esti Sheinberg (London: Routledge, 2017), 179.

19. Herbert Kellner, “Die Kunst der Fuga,” The Diapason 91, no. 5 (May 2000), 16.

20. Ibid.

21. In his article “Bach and Die Kunst der Fuge” (The Diapason, May 1998, pp. 15–17), Jan Overduin argues that downbeat quarter rests often symbolize death in Bach’s music.

22. As far as I am aware, the aforementioned observations were all previously undiscovered.

23. James Peter Burkholder, All Made of Tunes: Charles Ives and the Uses of Musical Borrowing (New Haven: Yale University Press, 1995), 138.

24. The notion of gradual revelation applies most aptly to the B-A-C-H theme, which occurs in only three movements: Contrapunctus VIII, in which its default form is inverted with repeated notes (i.e., most hidden); Contrapunctus XI, in which its default form is in rectus form with repeated notes (i.e., less hidden), and Contrapunctus XIV, in which it is finally stated plainly in Section 3.

25. I rounded to the nearest thousandth (0.417) so that one can see the numerologically significant part of the proportion (i.e., 0.41). If I had rounded to the nearest hundredth (0.42), its significance would have been obscured. This is not, however, a problem that Bach would have necessarily confronted. He would have solved these equations by hand, meaning he would see only as many decimals as he solved for, not the string of decimals that I see on a calculator. If he solved for only two decimals, he would have seen only “0.41.” After all, one only knows to round this number up to 0.42 if one also knows what the thousandth decimal is.

26. To the best of my knowledge, these proportional relationships were also previously undiscovered.

27. Gustav Nottebohm, “J. S. Bach’s letzte Fuge,” Musik-Welt, nos. 20 and 21 (1881): 2, http://ks4.imslp.net/files/imglnks/usimg/f/fc/IMSLP348435-PMLP562864-No….

28. Indra Hughes takes the final measure number, whose digits add up to 14, as evidence that Bach intentionally left the work incomplete and left a number of clues as to how it should be finished. See “Accident or Design? New Theories on the Unfinished Contrapunctus 14 in J. S. Bach’s The Art of Fugue, BWV 1080” (D.M.A. diss., University of Auckland, 2006), 20–21.

29. Indeed, the only other part of the work that could be said to be as harmonically daring is Contrapunctus XI.

30. Butler has since reversed this position, and now believes that the Fuga a 3 Soggetti was never intended to include Die Kunst der Fuge subject.

31. Gregory Butler, “Ordering Problems in J. S. Bach’s ‘Art of Fugue’ Resolved,” The Musical Quarterly 69, no. 1 (Winter 1983): 55, http://www.jstor.org/stable/741800.

32. Hughes, “Accident or Design?,” 84.

33. Hughes, “Accident or Design?,” 93–94.

34. Butler, “Ordering Problems in J. S. Bach’s ‘Art of Fugue’ Resolved,” 5.

35. Hughes, “Accident or Design?,” 86.

36. Ibid., 87.

37. This is because any combination will take as long as its longest theme. At six bars long, Theme 2 is the longest subject, meaning another triple combination would take at least six measures.

38. Hughes, “Accident or Design?,” 88.

39. A skeptical reader who double-checks my calculations may notice that Section 1’s 114.25 measures include the opening two beats of rest, even though I have not counted beginning rests in other movements. The original reason for this was that the calculations are much more exact if one counts 114.25 measures instead of 113.75, but this reason alone struck me as intellectually indolent. The realization though that 114.25 converts to 1141⁄4, and that counting those two beats makes Section 1 exactly 140 beats longer than Section 2 gave me some measure of peace with this decision.

40. In these calculations, it is important to start with the actual number of measures. For example, if one is determining the length of Section 3 from Section 2, then one should start from 55, not 55.035 or 54.997.

Sources

Burkholder, James Peter. All Made of Tunes: Charles Ives and the Uses of Musical Borrowing. New Haven: Yale University Press, 1974.

Butler, Gregory. “Ordering Problems in J. S. Bach’s ‘Art of Fugue’ Resolved.” The Musical Quarterly 69, no. 1 (Winter 1983): 55. http://www.jstor.org/stable/741800.

Hughes, Indra. “Accident or Design? New Theories on the Unfinished Contrapunctus 14 in J. S. Bach’s The Art of Fugue, BWV 1080.” D.M.A. diss., University of Auckland, 2006.

Kellner, Herbert Anton. “Die Kunst der Fuga.” The Diapason 91, no. 5 (May 2000): 15–17.

Milka, Anatoly P. Rethinking J. S. Bach’s Art of Fugue. Translated by Marina Ritzarev. Edited by Esti Sheinberg. London: Routledge, 2017.

Nottebohm, Gustav. “J. S. Bach’s letzte Fuge.” Musik-Welt, nos. 20 and 21 (1881): 2. http://ks4.imslp.net/files/imglnks/usimg/f/fc/IMSLP348435-PMLP562864-No….

Overduin, Jan. “Bach and Die Kunst der Fuge.” The Diapason (May 1998), pp. 15–17.

Wolff, Christoph. Johann Sebastian Bach: The Learned Musician. New York: W. W. Norton & Company, 2001.